One of my biggest gripes with the WaveFunctionCollapse procedural generation algorithm is that, despite the name, it doesn’t really have anything to do with quantum mechanics. I usually prefer the term Constraint Based Procedural Generation instead.
The name WaveFunctionCollapse is meant more as an analogy. As the algorithm progresses, it resolves a fuzzy, uncertain picture of the output into sharper detail, much as in quantum mechanics, the state of a system is also a range of possibilities, which resolves to something specific when “observed”.
But could we adapt WFC to the Quantum way of thinking, and ran it on actual Quantum Hardware? Well, that’s exactly what is discussed in this new paper Quantum WaveFunctionCollapse by Raoul Heese1 (Youtube summary). Does it work? Is it fast? Let’s find out.
“Classical” WFC
Let me briefly cover how a simple form of the WaveFunctionCollapse algorithm works. I have a longer article here.
The idea is that we want to generate a random map that is subject to certain constraints. The map will be a square grid of cells, and we want to fill each cell with a tile from a fixed set. The constraints are restrictions on what tiles can be placed next to each other. Typically, if you are imagining a level generator, you might want to ensure that the images on adjacent tile images seamlessly connect to each other.
The algorithm works by storing which tiles are “possible” in each cell of the map. Initially, every tile is possible in every location. Each step of the algorithm, it makes a random choice of a cell, and a possible tile for that location. Then via a process called constraint propagation, it eliminates some tile possibilities across the rest of the map. The process repeats until there is a unique possibility for the entire map. If you somehow end up with a cell with no possibilities remaining, then your choices so far have led to a contradiction, a map that cannot be completed while upholding all the constraints. You need to restart and try again with different choices.
It’s a neat algorithm – it’s simple to implement, easy to adapt for more complicated cases, and in practise it is rarely necessary to restart the generation. But it’s not especially fast.
A Brief Primer on Quantum Computation
So Quantum Mechanics is a fiendish subject, and I don’t propose to go into all of it here. Fortunately, Quantum WFC is one of the simplest possible algorithms, so we won’t need to go into all the details.
The basic unit of a quantum computer is a qubit. It is the equivalent to a bit in classical computing. A bit holds a single value, either a 0 or a 1. A qubit can also be thought of holding a 0 or 1. But the magic of quantum mechanics is that a qubit can also hold a combination of a 0 or a 1, called a superposition. For our purposes, we can think of a superposition as meaning, say: “30% chance of being 0, and 70% chance of being 1”.
Once you start having multiple qubits, you can start building superpositions that involve multiple bits. For a 2 qubit system, you could have a superposition “20% chance of 00, 10% of 01, 30% chance of 10, 40% chance of 11”. So a 2 qubit system holds the probabilities for 4 distinct states. A \(n\) qubit system would hold probabilities of \(2^n\). This is what makes Quantum Machines so powerful – even a small number of qubits can hold an exponential amount of information.
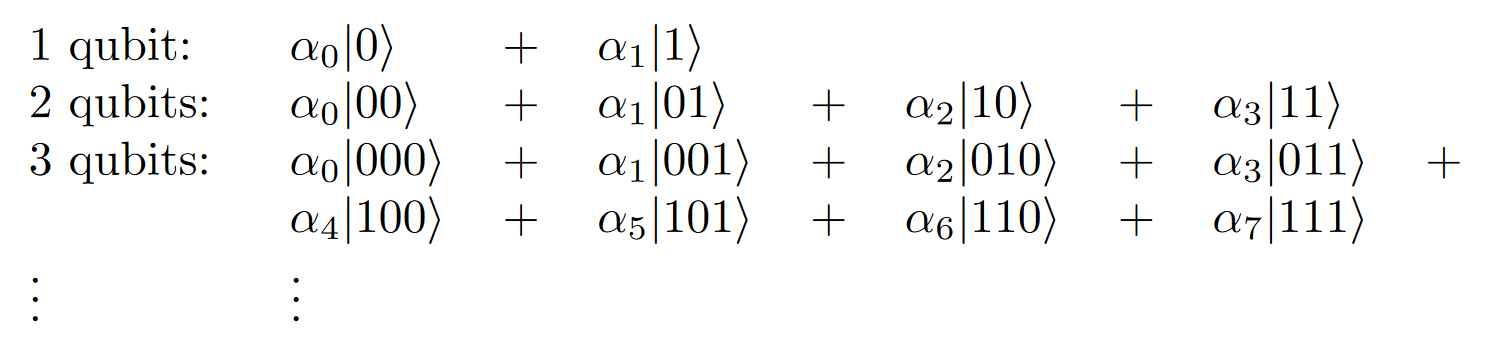
To build these superpositions, qubits are combined with each other via various quantum gates, arranged in a circuit. These are very similar to the classical logic gates like NOT, AND, OR and XOR that are used in normal circuit design, but they are always reversible. There’s a wide variety of gates, we won’t go into their exact details.

Most quantum algorithms are very complex, as even though you have the tools to build superpositions that “store” a great number of different probabilities, and have gates that can efficiently act on all those probabilities simultaneously, it’s hard to actually extract any useful computation from the system. The algorithms typically arrange for some constructive/destructive interference, so that probabilities associated with the correct answer are boosted, while probabilities associated with wrong answers are shrunk. Then you can make a measurement, which reads a random state of the qubits from the superposition, destroying the superposition in the process. The random state will likely be correct, and the process can be repeated multiple times to gain an arbitrary level of confidence. This is the quantum advantage of this sort of computing.
Quantum WFC doesn’t work this way. There are no interference effects, instead it simply builds a superposition where all the probable states are solutions to the generation, and randomly picks one via the measurement process. This is merely a probabilistic advantage.
The Quantum WFC Algorithm
In the paper’s terminology, each cell of the grid is called a “segment”, and the possible tiles are the “value” of that segment. If there are \(2^q\) distinct tiles (or fewer), then we need \(q\) qubits per segment to store the values. There are \(N\) segments in the grid, so we need \(N q\) qubits in total. The number of qubits is a critical number – as we can’t actually build quantum computers with larger numbers of qubits. The device the author used had only 127 qubits available, and some of those go to waste.
Now we’ve got the storage layer sorted, we need to build a circuit of quantum gates that builds the superposition.
This is done iteratively. We fix an ordering of the different segments at the start – the paper uses a snake pattern. I’ve experimented with different orders in classical WFC and it seems the ordering makes relatively little difference to results.
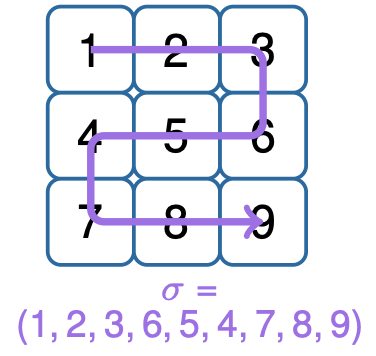
Before the iterations, we starts with all the qubits initialised to \(\left|0\right>\), which simply means 100% probability of being 0. The superposition is empty. At each iteration, we add combine one more segment into the superposition, using gates to ensure that the value of the new segment and the values of the previous segments are mutually consistent with the rules of the constraints. The combined circuits from each the iteration are put in a long chain forming the ultimate circuit that describes the algorithm.
Because constraints between segments are only for adjacent segments, we see a similar pattern in the circuits – there will only be gates combining the qubits of two segments if they are adjacent. This helps keep down the total number of gate operations required.
So what gates exactly are needed in each iteration? There’s two different sets of gates.
The first set, the initialisation gates, are responsible for taking the initial state of the segment’s qubits, and setting up a probability distribution of values. For WFC, this is often a uniform distribution, but some variants allow a weighted distribution. With the right set of gates, any probability distribution can be set up in the superposition, though it can require a lot of gates.
The second set of gates, are the control gates. These enforce the constraints between adjacent segments. Suppose you have rules that values 0 and 1 can go above value 0, and values 1 and 2 go above value 1. And say that segment 6 is directly above segment 9. Then you’d need one set of gates that detects if the qubits in segment 6 are 0 or 1, and if so, conditions the qubits of segment 9 to be 0. And similarly a set of gates that detects values 1 or 2, and conditions the cubits to be 1.
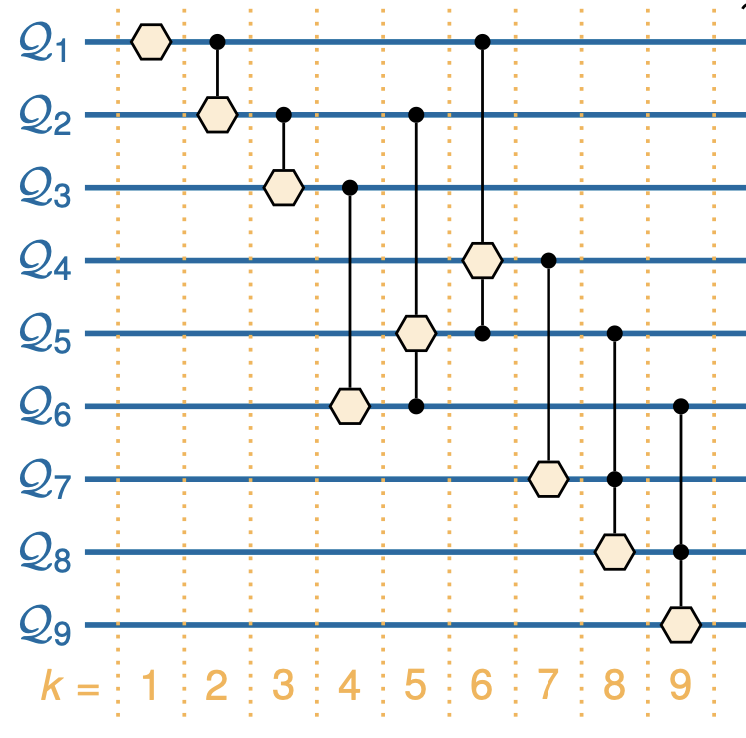
The control gates basically ensure that the probability distribution of the segments computed so far is, plus the adjacency requirements for the new segement, give a new probability distribution with one more segement. So these gates are roughly analagous to the constraint propagation step of classical WFC.
Like the classical case, propagation gives the algorithm some “smarts” – it aims to pick states that fulfil the adjacency constraints. And like the classical case, it is not perfect – in harder cases, it’s still possible for contradictions to occur, which forces the algorithm to start over.
Classical WFC can apply the adjacency in either order, while Quantum WFC only applies the adjacencies forward from earlier segments to later segements. As a consequence, Quantum WFC is a bit more prone to contradictions and can be unreliable in some cases. The hope is that the quantum machine is so fast, you can simply just afford to run it multiple times in search of a solution2.
Hybrid QFC
The author also proposes a hybrid scheme that is part quantum, part classical, to save on qubits and circuits and improve reliability. I won’t dwell on this as there are a number of partitioning schemes for WFC already, and they are most details about trading off various shortcomings.
Results
One of the cool things the author actually ran this on a real quantum computer. The IBM Eagle chip came out in 2021, and holds 127 qubits – a record breaking amount at the time. These chips are still very rare and expensive – Raoul got some time on IBM’s cloud services to try it.
127 bits is not very many. In his simplest possible example – generating a chequerboard pattern on a 3×3 grid, only 9 bits are needed. But the next example had 8 tiles on a 4 by 10 board, this requires \(3 \times 4 \times 10 = 120\) bits, essentially the entire computers memory. Hence the need for the hybrid computation.
The other problem with real quantum machines is they are not reliable. Keeping qubits in a state of quantum superposition is very difficult from a physics perspective, so they have a small chance to randomly do the wrong thing. The larger your circuit, the more this problem becomes acute.
So while the algorithm worked in a simulator, in the real thing, the results are less than ideal:
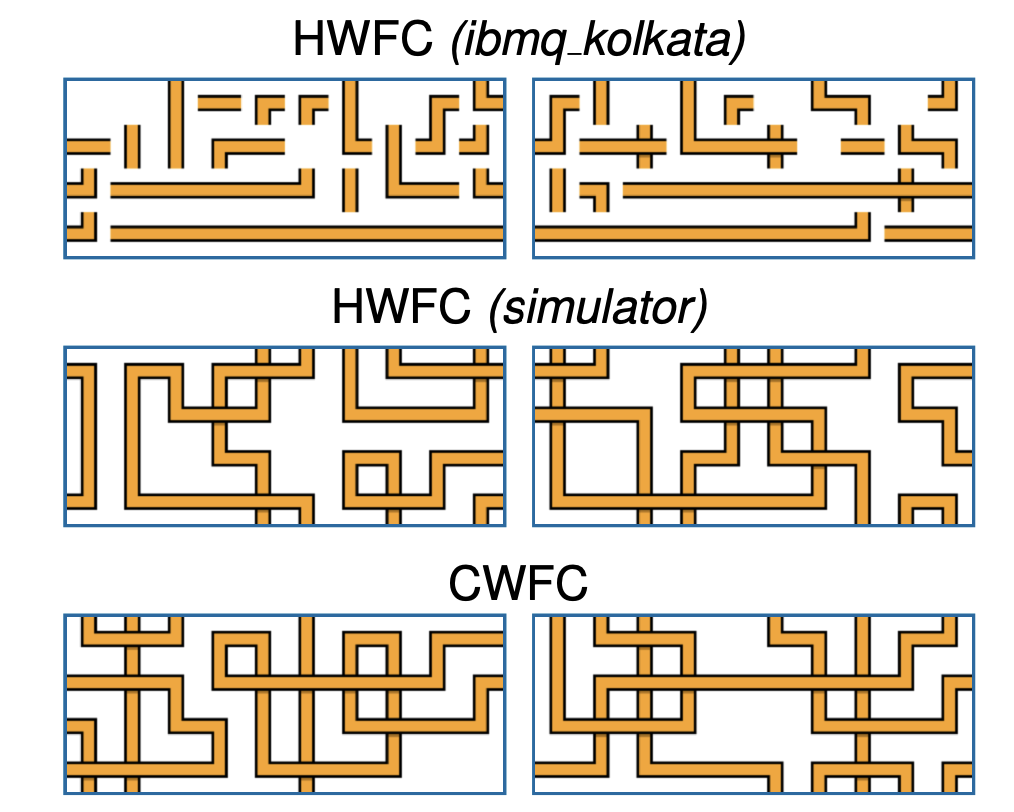
To be fair, almost all quantum research is like this. Researchers are designing algorithms now to be used in the near future when we have machines of greater reliability and number of qubits. Until then, it’s necessary to run the same calculation many times. The paper repeated everything 10,000 times.
So I’m not convinced that Quantum WFC is going to replace the classical algorithm any time soon. But I feel better know that there is some solid foundational reason for how the classical algorithm relates to quantum mechanics. It really is true that classical WFC has a fairly “natural” translation to real wave functions, which is exactly what the naming implies.
My other disappointment was that the algorithm only takes advantage of the probabilistic computation features of quantum computers. There’s no actual quantum magic, the sort of stuff that gives exponential (or quadratic) speed-ups. There are other quantum algorithms out there for constraint solving that I feel could be adapted for WaveFunctionCollapse, which at least on paper can offer algorithmic improvements for hard tile sets beyond what is outlined here.
- Thanks to Raoul for reviewing a draft of this article and supplying some diagrams. ↩︎
- Tile adjacency in general is an NP problem, and WFC is not a state of the art constraint solver. So if you are giving very difficult problems with lots of contradictions to either Classical or Quantum WFC, you are probably not going to have a good time. ↩︎