I’ve been working on adding aperiodic grids to Sylves.
Aperiodic tilings are made tilings are made of a fixed set of tiles, rotated and translated to fully cover the plane.But they are not periodic – there’s no way to rotate/translate the whole grid onto itself.
This makes them almost hypnotic in their balance of regularity and chaos. A classic example is the penrose tiling.





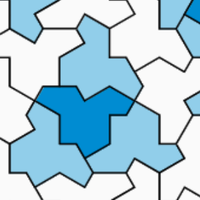
Table of Contents
Substitution Tilings
My implementation uses a substitution system to generate them. The other common approaches, multi-grids and cut-and-project, will have to wait for another time.
The idea behind substitution tilings is that you start with a single tile, then alternate two steps. “Dissect” cuts the tile up into a smaller set of tiles. Then “Inflate” scales everything up so the tiles are back to their original size. Here I demonstrate with the chair tiling which is one of the simpler tilings of this type.
This process can be repeated indefinitely
Eventually you get an infinite amount of tiles.
Many different tilings can be made this way. Here are the rules for the Penrose Rhomb tiling1
It’s a lot more funky!
- Now there are two different sorts of tiles (thin and fat rhombuses). I’ve colored them differently for clarity.
When we dissect a thin tile, we get one thin, and one fat, while dissecting a fat tile gives two fat tiles and one thin. - The dissections aren’t perfect: the smaller tiles don’t exactly stick to the boundary of the larger tile they were dissected from. We should properly call the dissections substition rules to reflect their generality.
- The scaling used for inflation (the inflation factor) is irrational (\( \frac{1+\sqrt{5}}{2} \))
Nonetheless, if you repeatedly disect and inflate, you get a full tiling.
Implementation in Sylves
My implementation of substitution tilings diverges from this basic plan in a number of ways. Sylves grids are designed to be efficient for use in games. That means, they don’t consume a lot of memory, and they support lots of common operations. I’ll discuss how I made those work for substitution grids. It’s based on ideas described here.
Lazy Trees
I’ve tried to make every grid in Sylves efficient enough to work for use in games. But you’ll notice that every step of the dissection increases the tiles in the grid exponentially. For the chair tiling, first you need 1 tile, then 4, then 16, and so on. What we need is a way of lazily generating tiles as we go.
The trick is to arrange the tiles in a infinite tree structure. It’s similar to what i describe in Infinite Quadtrees. The idea is that the starting tile is at the bottom of a tree. Doing an inflation corresponds to moving up the tree by one node, and doing a disection corresponds to finding all the children of a node. All the actual tiles are at the bottom of the tree, other nodes correspond to “prototiles” – which are inflated versions of the tiles themselves.
You can locate any tile in the tree by doing several inflations, then several disections, choosing a single prototile from each disection. It doesn’t matter that we are no longer alternativing inflations and disections – as long as there are equal amounts of both, we’ll end up with tiles.
This lets you evaluate any tile, without having to fully dissect the entire tree.
Tile Labels
This same trick has a lot of other conveniences. You can use it to assign a unique label to each tile, based on the path from the root of the tree down to the tile you want. E.g. in the diagram above, the path to the starting tile on the left is (0, 0) as it’s the first child (0) of the first child (0) of the root. But the tile on the right is the second child (1) of the third child (2) of the root, so it has path (2, 1).
Of course, I only drew a tree of height two, but I could have done more inflations to get a larger tree. So we’ll implicitly consider every path as starting with an infinite amount of zeros. So the path of of the tile is more like (…., 0, 0, 2, 1).
In the chair grid, as ever node of the tree has 4 children, we could encode the whole path into a single number, using base-4 counting: The encoded path is \(2 \times 4^0 + 1 \times 4^1 + 0 \times 4^2+\cdots = 6 \). Sylves uses these integers as the unique label of each tile.
Finding Tiles
It’s not enough to know where any given tile is located. I’m also interested in the inverse operation: at a given location, which tile can be found there. This is called cell picking.
There’s a fairly straightforward way of doing it. We can inflate the starting tile until we’ve got a tile large enough to cover the point we’re interested in. Then repeatedly disect it, choosing the child each time that contains the point. The path followed indicates the tile. Due to the exponential growth of the tree this only requires a logarithmic number of steps, as the distance from the origin increases.
In practice, I never wrote this code. Instead, I wrote code to find tiles in a region (described below), then ran it for a zero-sized region.
Searching Tiles
What really did my head in was searching for all tiles that intersect a given rectangular region. I couldn’t find any closed formula for this, so again, need to do a tree search.
You want to do the same thing, walk up the tree, then walk down it again. But this time there are multiple valid paths. Ok, then, we can do a depth first search. But that doesn’t work either! Remember, the tree extends infinitely high, so you need to know how high to set the root node, and I couldn’t find a satisfactory way of doing so.
In the end, I opted for a 2 step solution. First, I collect a set of nodes I’m calling the “spigot“. The spigot is formed by walking up the tree, and adding all children of the nodes encountered, except the node just walked from. It’s technically an infinite set as we can go higher and higher in the tree with more inflations.
The spigot set has several properties.
- The descendants of the spigot nodes cover every leaf node (the tiles) exactly once.
- It can be iterated over linearly
- Successive spigot nodes covers larger and larger chunks of the tree.
Here’s the spigot nodes shown for the chair tiling. There’s a few small tiles, but the tiles rapidly get very big. That’s what makes it an efficient search.
The second step is to iterate over the spigot nodes, and do a depth first search on each of them. Basically, you test the node’s aabb against the rectangle region. If it matches, add all the disection children to a stack. You can keep testing and subdividing stack items until you reach leaf nodes that can be outputted.
As the spigot set is infinite, you need to know when to stop. I track if any tiles were found from the current node. If there have been none for sufficiently many items in the spigot, then I conclude it has run dry, and stop.
I apply a similar trick for raycasting – find the spigot nodes, and subdivide if they intersect the ray. Some careful book keeping is required to output the tiles in order, and determine if/when the spigot runs dry. As the ray is infinite and so is the spigot, this can produce an unending stream of raycast hits as you walk along the ray.
Translation Issues
In the maths of a inflate-disect tiling, translation is kinda ignored. It’s not really relevant as you don’t need to line up multiple steps of the algorithm.
But with a lazy tree approach, we explicitly want it so that as extend the tree upwars, the nodes line up with the tiles already generated. Further, the tile labels I’m using require that the first child of the disection of an inflation is the original tile inflated from.
These requirements dictate what translation is done by the inflation. For some tilesets, it won’t spread out in all directions. Meaning you can end up with an infinite amount of tiles, but still some “blank space” that is never filled with tiles:
To resolve this, I’ve had to double the substitution rules of most tilings so that first child of each node isn’t always in a consistent position. By alternating the two rules, we ensure outward growth occurs in all directions, again inspired by my Infinite Quadtrees article.
What’s next?
Sylves’ implementation still needs some work. Nearly every operation is done now, and most of them are logarithmic runtime, or constant time with a cached tree.
Unfortunately it’s very tedious to actually input the tilings. At present I’ve only done a handful. Contributors welcome!
Maybe then I’ll get to implementing the other main source of aperiodic grids, the multigrid method. It makes less regular structures but often has a pretty radial symmetry.
- These are likely slightly different to the rules you normally see. I’ve omitted some tiles that cause duplicates to appear. ↩︎
