procgen

Fiddling Weights with Temperature

| Boris

In procedural generation, the absolute simplest, most common technique is randomly picking an item from a list. More often than not, it is a weighted random choice, where each item is selected with a frequency proportional to its “weight”, a numerical value that can be tweaked by the designer.

def random_choice(items: list, weights: list[float]):
    total_weight = sum(weights)
    random_value = random.random() * total_weight
    
    # Find the item that corresponds to the random number
    for i, weight in enumerate(weights):
        random_value -= weight
        if random_value <= 0:
            return items[i]

I wanted to share a technique from the Machine Learning community that is simple enhancement to this routine that gives a lot of convenience over tweaking weights directly, called temperature.

Continue reading →

Exploring Rectangle Subdivisions

| Boris

Last week, I saw a talk on Vuntra City, a procedurally generated city with a fully explorable city. Developer Larissa Davidova explained that she settled on using Recursive Subdivision for the city blocks, as she wanted some level of organicness, while still only having to deal with rectangles. But she didn’t like having indefinitely long roads that cause implausible sightlines.

One way Vuntra City handles this is by subdividing a rectangle into 5 blocks, a pattern I called “whirl” in my previous article on recursive subdivision. You can see that it has no internal roads that stretch across the entire map.

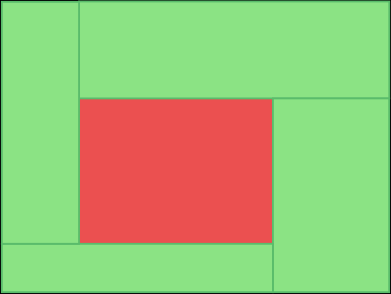
But Larissa’s talk got me thinking. The whirl pattern is interesting because it cannot be made from simple cuts. What other ways of subdividing a rectangle into smaller rectangles1, are out there?

Continue reading →

Running Tracery bots with LLMs

| Boris

Tracery bots were a fun, simple, way of making generative texts. They are basically an easy way to specify generative grammars via a simple JSON file format. There used to be a horde of fun little tracery bots on twitter until API changes shut them all down.

Darcy is saying "You are well-educated, but no cromulent enough to intrigue me"

Nowadays, you can prompt a chatbot to get whatever you want. But that lacks the same charm, and it doesn’t give you the control you’d want for something unleashed on the internet. Let’s do something about that.

Continue reading →

Generating Tilesets with Stable Diffusion

| Boris

Recently I’ve been playing around more with gen AI techniques. I thought I’d try to generate a set of tiles that all connect together. It’s harder than it sounds – Stable Diffusion is hard to control, so there’s no easy way to get a set of images that are fully consistent with one another.

I’ve developed a technique for doing it that I’ll call Non-Manifold Diffusion as it involves doing diffusion over a set of patches that interlock to form a non-manifold surface.

Continue reading →

My Mental Model of AI Creativity – Creativity Kiki

| Boris

I went to some lectures on the future of science in games recently, and the keynote speaker was Tommy Thompson, an well-known AI expert in the game dev space.

Of course, by AI, he didn’t mean the modern sort that dominates the news. His focus is AI for games, which is algorithmic and rarely involves any ML component. Still, he spoke about the challenges the industry faces regarding Image Generators, LLMs and so on. He specifically called LLMs “stochastic parrots”, which I found disappointing. Imho it’s an incredibly misleading model of what LLMs are capable of and is usually deployed to downplay their abilities and belittle them. But it’s a common view, particularly in creative industries.

So what is a better model? It’s clear that they are not that smart in most ways we consider important, but they do have some interesting capabilities. Here’s model I use that I feel give a better intuition for what they can and cannot do.

Continue reading →

Substitution Tilings

| Boris

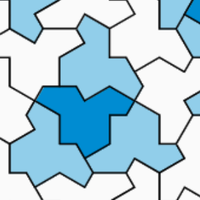
I’ve been working on adding aperiodic grids to Sylves.

Aperiodic tilings are made tilings are made of a fixed set of tiles, rotated and translated to fully cover the plane.But they are not periodic – there’s no way to rotate/translate the whole grid onto itself.

This makes them almost hypnotic in their balance of regularity and chaos. A classic example is the penrose tiling.

Images from the Tiling Encyclopedia
Continue reading →

Quantum WaveFunctionCollapse

| Boris

One of my biggest gripes with the WaveFunctionCollapse procedural generation algorithm is that, despite the name, it doesn’t really have anything to do with quantum mechanics. I usually prefer the term Constraint Based Procedural Generation instead.

The name WaveFunctionCollapse is meant more as an analogy. As the algorithm progresses, it resolves a fuzzy, uncertain picture of the output into sharper detail, much as in quantum mechanics, the state of a system is also a range of possibilities, which resolves to something specific when “observed”.

But could we adapt WFC to the Quantum way of thinking, and ran it on actual Quantum Hardware? Well, that’s exactly what is discussed in this new paper Quantum WaveFunctionCollapse by Raoul Heese1 (Youtube summary). Does it work? Is it fast? Let’s find out.

Continue reading →

What Is Procedural Generation

| Boris

Procedural Generation can be interpreted quite broadly as just “making computers make cool creative things”. People make art, games, music, audio, stories and all sorts of weird things.

I’ve been doing it as a hobbyist for some time, and have become more and more involved: I make tutorials, projects, I sell a tool online for a niche algorithm, and recently taught a “masterclass” at Everything Procedural, the main conference for professionals in the space.

I thought I’d spill some digital ink about what it’s actually about. I get asked often enough, and this will help me clarify my verbal answers.

Continue reading →

Generative Generators

| Boris

This is a experiment I tried out for ProcJam 2023. I wasn’t getting great results from it and got bored after a few days, but I’ve decided to share what I did manage.

The rules of the hackathon were changed this year, ruling out most forms of AI. I was thinking – what’s the furthest I can push that rule without crossing the line?

In the end, I designed a system where we used AI to design and build a standalone classical generator.

Continue reading →