Last time, we looked at quarter-tiles. This was an auto-tiling technique for square grids. Each cell in the grid is associated with a terrain (i.e. either solid or empty). Then the squares were split in four, and each quarter was assigned an appropriate quarter-tile.

Otho-tiles extends this procedure to work with irregular grids, even non-square grids. We just have to alter the procedure a little, and be ready to deform the quarter tiles fit in place.

Ortho?

Ortho is a Conway Operator. It can be thought of as the extension of dividing a square into 4. It divides each n-gon into n “kites” or “ortho-cells”. Each kite is a four sided shape containing the cell center, one corner, and the midpoint of the two edges adjacent to that corner.

The appeal of the ortho operation is it can take any polygonal grid, no matter how irregular, and convert it into a grid of 4 sided shapes. And it’s much easier to work with something that has a consistent number of sides.

Continue reading →

Since Oskar posted about it, I see an increasing amount of praise for his Dual Grid proposal for autotiling terrains. It works by drawing tiles at a half-cell offset to the base grid, creating a dual grid, and using marching squares autotiling to select which tile to draw based on the terrains the corners of the dual grid, which is the centers of base grid.

More talk prep. Gonna have another go at persuading people to cut their tiles along the dual grid instead of the main grid. I genuinely don't understand if this is rare because people don't know about it or if there is some drawback I'm not seeing. pic.twitter.com/nm4aDLAesT

— Oskar Stålberg (@OskSta) October 13, 2021

This is a great scheme. It’s simple, only needs a few tiles and can be extended quite easily. It’s used in many games.

But, it does have some drawbacks. The dual grid is difficult to get your head around. You have to worry about ambiguous tiles. And despite being a substantial improvement over the blob pattern, it still requires drawing quite a number of different tiles.

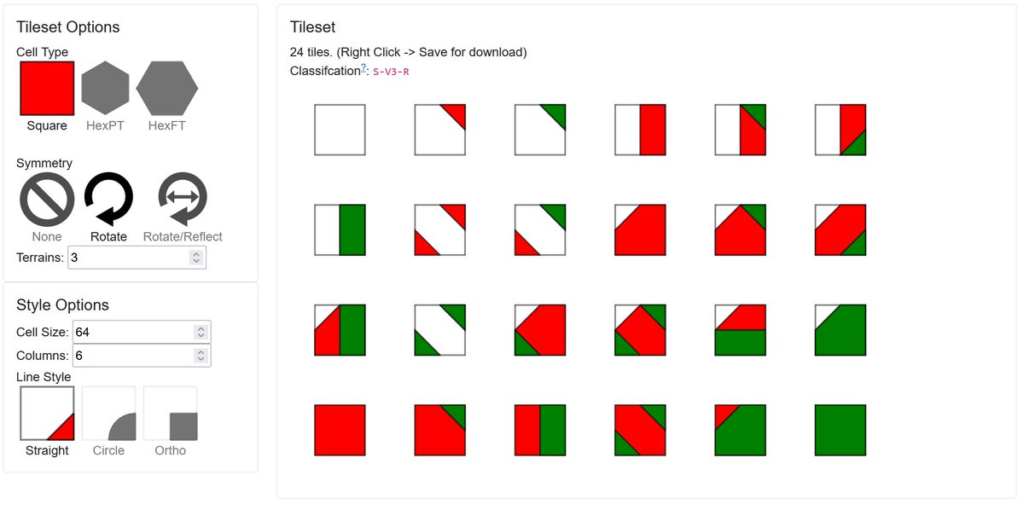
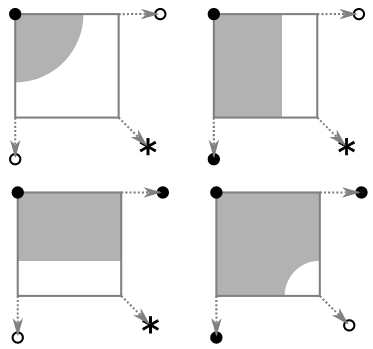
I’m here to explain an alternative, quarter-tile autotiling. Quarter-tiling has also been called sub-tiles, meta-tiles (when doubling instead of halving). I’ve previous described as micro blob, which is the same thing with precomposition. It’s best known for being the tiling built into the RPG Maker engine.

Quarter-tiling is pretty easy to implement, and requires substantially less effort to create tiles for, as it uses fewer, smaller tiles. That does mean it’s not possible to produce as much tile variation as marching squares. But there’s plenty of techniques for adding that back.

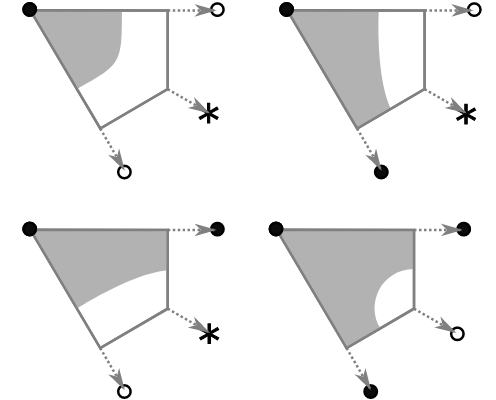
Later, we’ll look at ortho-tiles – an extension of quarter-tiles to irregular, non-square, grids.

Continue reading →