Hamming Weight
The Hamming Weight of a binary number is simply a count of the number of 1's it contains. So the Hamming Weight of 100001 is 2 and 1101 is 3. It is named after Richard Hamming and is used in several logic disciplines including cryptography. Read more at Wikipedia.
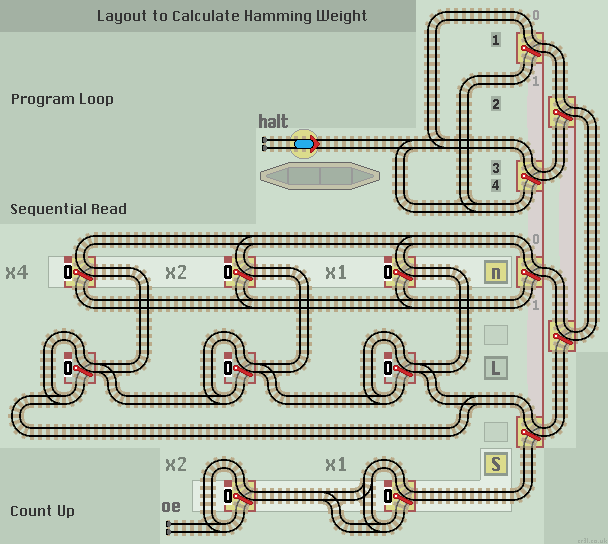
The Hamming Weight is calculated by using a Sequential Read and a Count Up (incrementer) function.
Operation
- Clear the S and L registers and set register n to the input number.
- Run the train. When it returns to the station, register S will show the Hamming Weight of n.
|
| Click layout to pause/run train | Click points to switch 0/1 | Click start circle to reset train/points |
| Lazy points switch between upper 0 or lower 1 branch lines Trains arriving on a branch line switch the point to that line |
|
| Sprung points allow branch line trains to join the main line All main line trains go straight ahead and never 'branch off' |
How it works
Each data bit is read out in turn. If it is a 1 the counter is incremented. The program loops back to the start to read out the next data bit. When all bits have been read, the program halts.
The S and L registers are reset to 0 before each new calculation. The counter should never overflow as the maximum number of 1's the n register can contain is 3.
Note
Also see Hamming Weight function which is more efficient as the train passes on immeadiately if a data bit is a 0. This illustrates how a dedicated function is usually faster than a general computer layout of program loop and functions library.